Nel corso dell’ultimo decennio, le nuove tecnologie e la digitalizzazione hanno iniziato ad avere un notevole impatto sulle industrie di processo tradizionali che coinvolgono liquidi, come quelle che si occupano di trasporto e trattamento di acqua o di acque reflue. Poiché queste interessanti applicazioni sono ormai più realistiche e disponibili, team di ricerca dedicati in ABB sono al lavoro per garantire ai clienti gli strumenti migliori e più economici per migliorare il proprio vantaggio competitivo.
La tecnologia dei digital twin può fare proprio questo, poiché permette di individuare precocemente eventuali problemi fisici e di prevedere con precisione i risultati. Con lo sguardo rivolto al futuro, ABB ha colto l’opportunità di utilizzare questa tecnologia per migliorare i propri prodotti di flussometria, in modo da soddisfare le sfide di processo, generare valore ancora più velocemente e soddisfare le aspettative sempre più alte dei clienti.
Flussimetri elettromagnetici
I processi di produzione richiedono una strumentazione affidabile e precisa per soddisfare elevati standard di prestazione.

Da oltre 40 anni ABB è un partner affidabile per l’industria idrica mondiale grazie al suo impegno nello sviluppo di prodotti, system solution e servizi. I flussimetri di ABB sono da sempre cavalli di battaglia nell’industria dei processi produttivi perché sono robusti, affidabili e, soprattutto, accurati (Figura 1A).
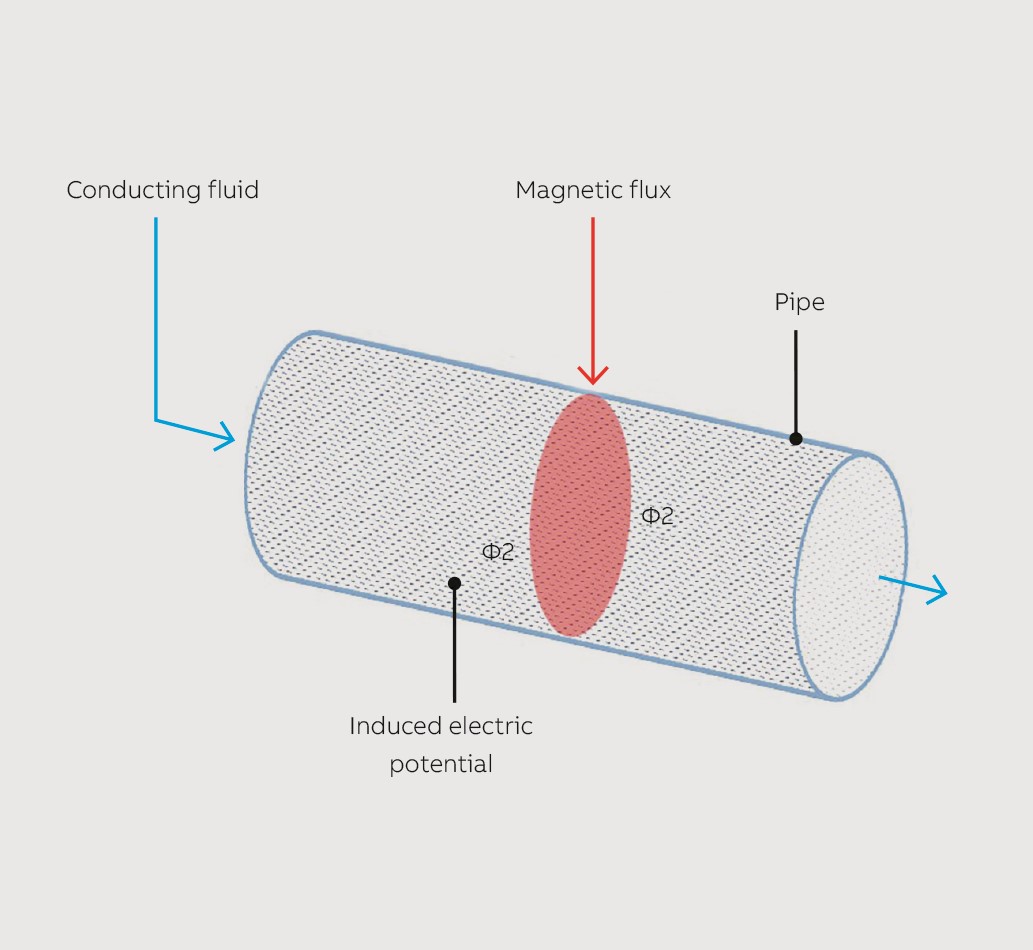
FIGURA 1. (A) Il flussimetro EM di ABB. (B) L’interazione fra il flusso magnetico e il fluido conduttivo in movimento induce un potenziale elettrico (Φ2) proporzionale alla velocità del fluido Φ1 – Φ2.
I flussimetri EM, che costituiscono una parte importante dei prodotti offerti da ABB per la misurazione del flusso, sono particolarmente interessanti per i clienti che trasportano o trattano liquidi conduttivi, poiché presentano una serie di vantaggi unici: semplicità di installazione, impatto trascurabile sulle perdite di carico e alta precisione. Inoltre, le prestazioni dei flussimetri EM non sono sensibili a variazioni di temperatura, pressione o densità, né sono influenzate da piccole fluttuazioni dei profili di flusso. Indipendentemente dalla direzione del flusso, con errori di misurazione contenuti entro ±0,2% su ampi campi di portata, i flussimetri EM consentono una misurazione accurata a basse portate.
Combinando una profonda conoscenza della fisica dei misuratori di portata con nuove tecniche di modellazione verificabili, ABB lavora per aggiungere valore ai flussimetri esistenti.
Il concetto di digital twin
E se si potesse sviluppare un modello predittivo basato sulla conoscenza dei processi fisici, capace di prevedere le prestazioni di un flussimetro e ridurre al minimo la necessità di test? Il risultato sarebbe una produttività senza precedenti e prestazioni più elevate. Per ottenere questo risultato ABB ha sviluppato il modello digitale di un flussimetro EM basato su una tecnica di analisi multifisica agli elementi finiti (FEA). Questo modello, o digital twin, è una replica che rappresenta l’oggetto fisico nel mondo virtuale, imitandone così il comportamento reale. In questo modo è possibile comprendere le complessità delle prestazioni, individuare i problemi e migliorare i progetti sulla base delle conoscenze acquisite sul processo. Queste informazioni possono essere utilizzate successivamente per costruire e utilizzare il prodotto sul campo.
ABB ha scelto il modello multifisico di un misuratore di portata EM per migliorare la sua già eccellente offerta di flussimetri.
Integrazione dei fenomeni fisici
Inizialmente è stata costruita la geometria di un flussimetro utilizzando un software CAD (Figura 2A). La geometria, o dominio computazionale, è stata poi discretizzata in minuscoli elementi nei quali sono state risolte le equazioni fisiche (Figura 2B). Sono stati modellati diversi campioni di flussimetri di varie forme e dimensioni (Figura 3).
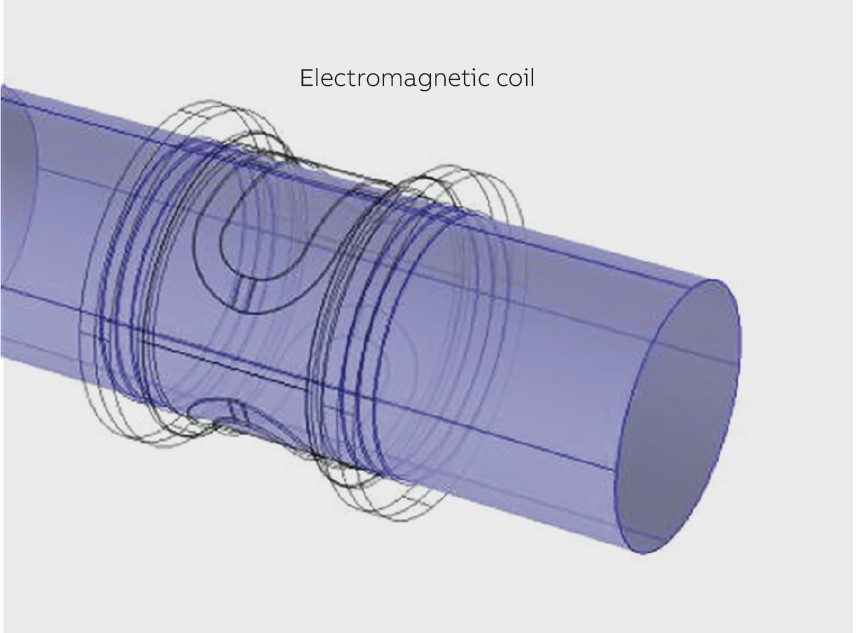
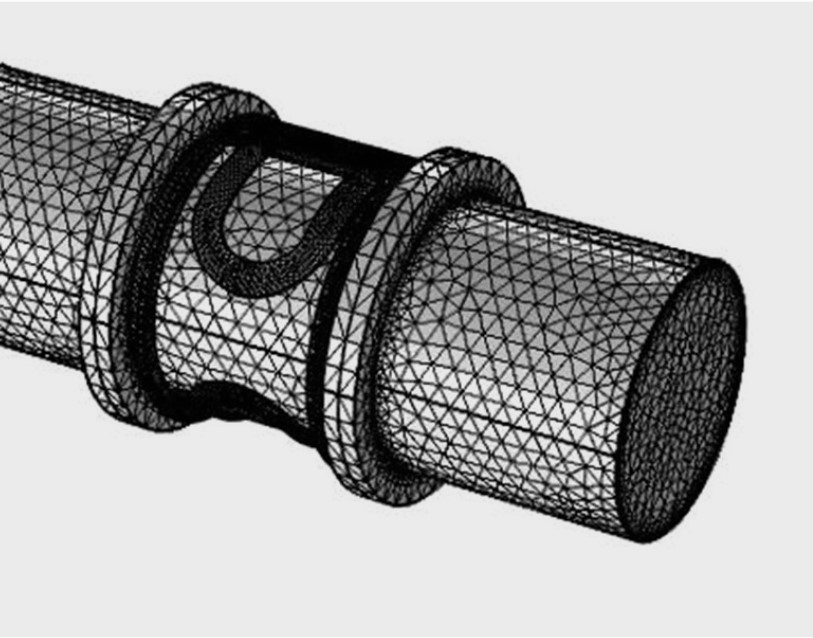
FIGURA 2. (A) Geometria del flussimetro EM costruita con un CAD. (B) Geometria discretizzata per i calcoli FEA.
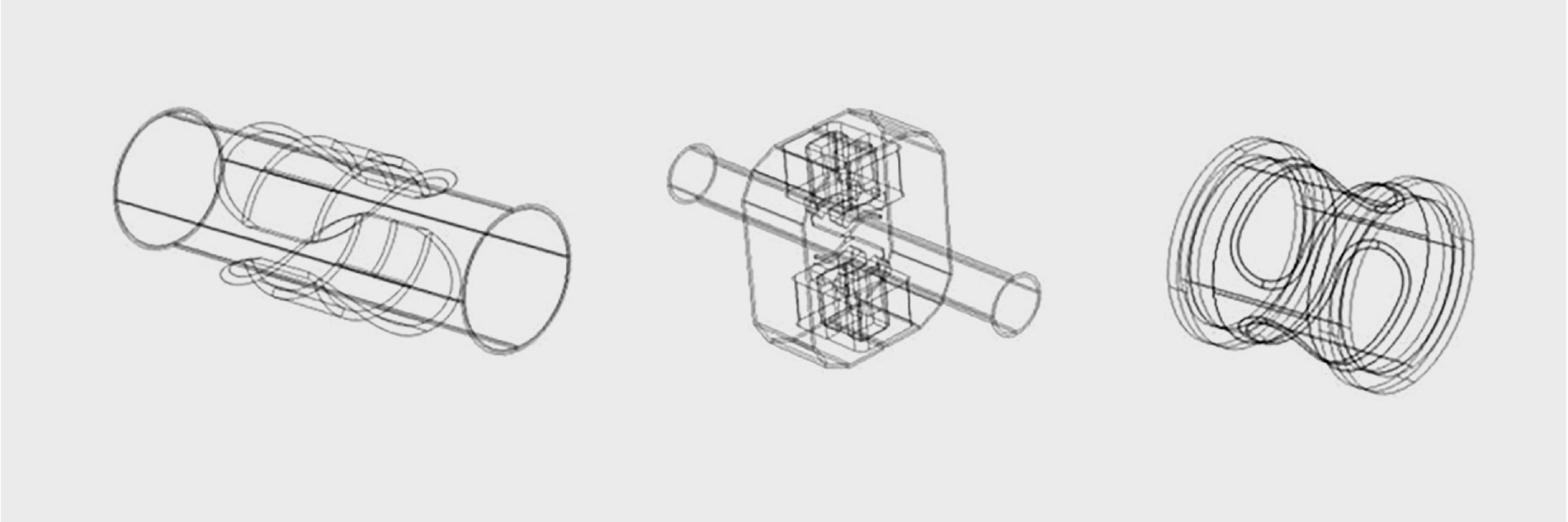
FIGURA 3. Modellazione di diverse tipologie di flussimetri, che differiscono per la forma e/o per le dimensioni dei componenti.
L’integrazione dei due fenomeni primari, elettromagnetismo e fluidodinamica, con altri fenomeni fisici all’interno di un unico modello è impegnativa. L’elettromagnetismo viene analizzato risolvendo le equazioni di Maxwell, che inizialmente calcolano la densità del flusso magnetico all’interno del dominio computazionale (Figura 4A). La fluidodinamica viene studiata invece risolvendo le equazioni di conservazione della massa e della quantità di moto per varie condizioni di flusso, simulando il flusso del fluido attraverso il tubo (Figura 4B). In seguito l’EMF indotta, risultato dell’interazione tra flusso magnetico e velocità del fluido, viene calcolata integrando i campi magnetici e il flusso, utilizzando le equazioni di Lorentz derivate dalla legge di Faraday dell’induzione elettromagnetica (ved. Figura 4C). Il risultato principale è la sensibilità, o il rapporto tra EMF indotta e velocità del fluido.
Per ottenere un quadro completo, il modello calcola anche i parametri di propagazione termica e di dinamica strutturale. Vengono analizzate le sollecitazioni termiche e idrauliche che agiscono sulla parete del tubo (Figura 5). Simulazioni tanto avanzate sono essenziali per prevedere l’effetto di condizioni difficili e avverse sull’integrità del flussimetro.
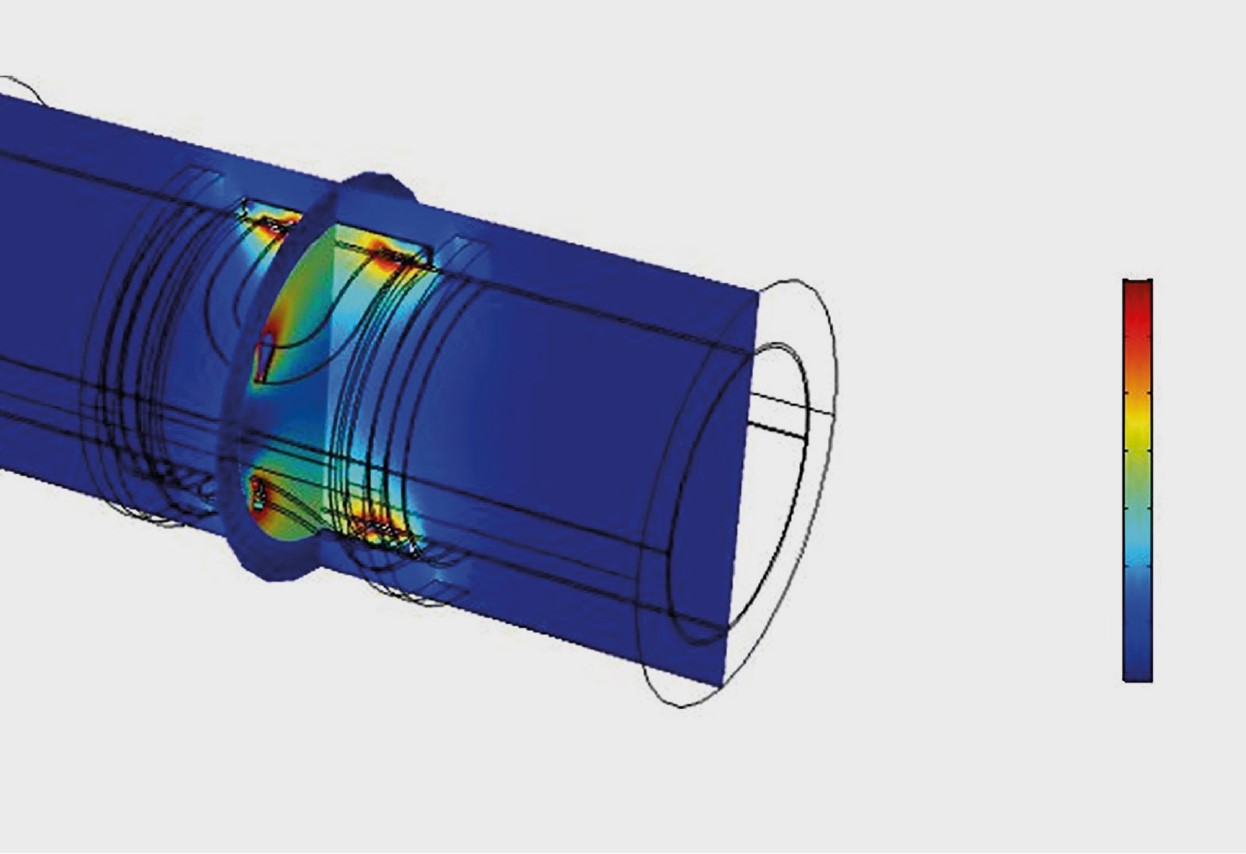
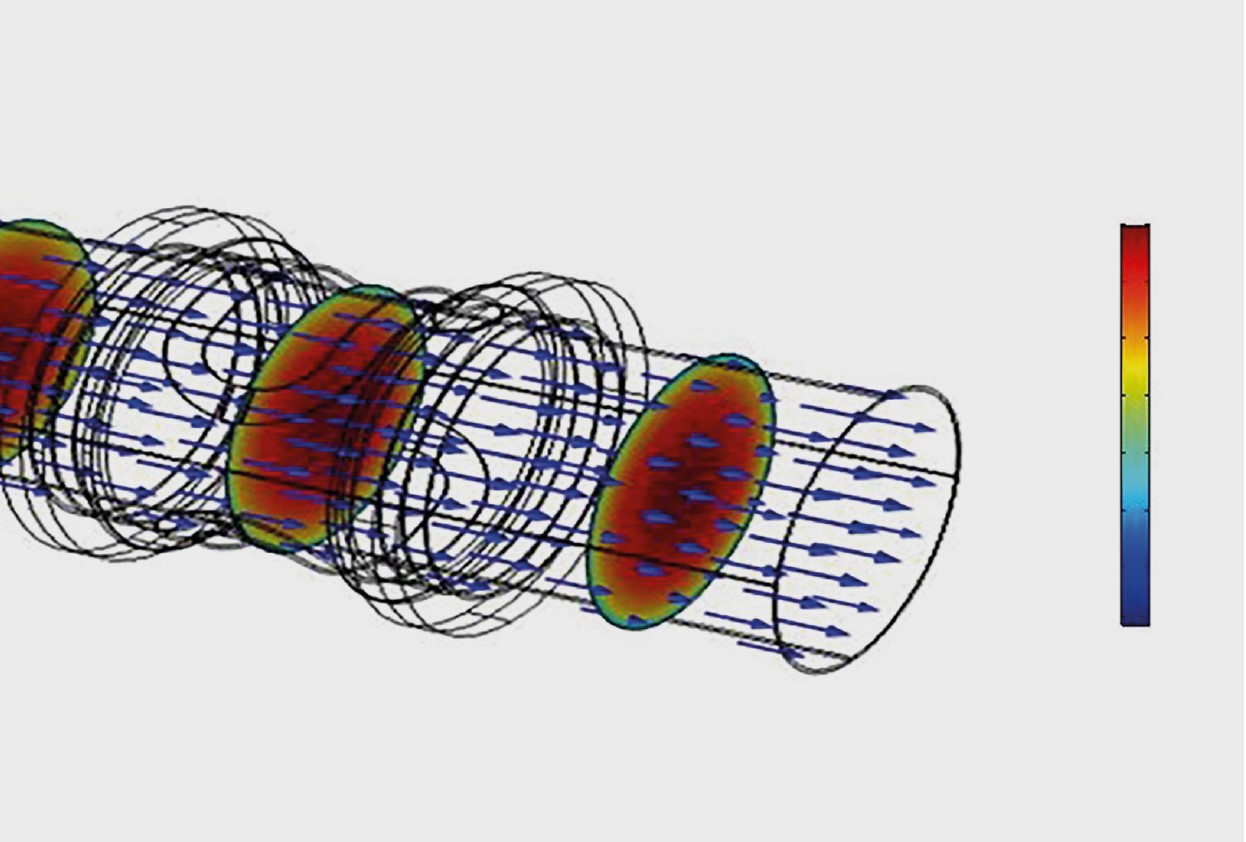
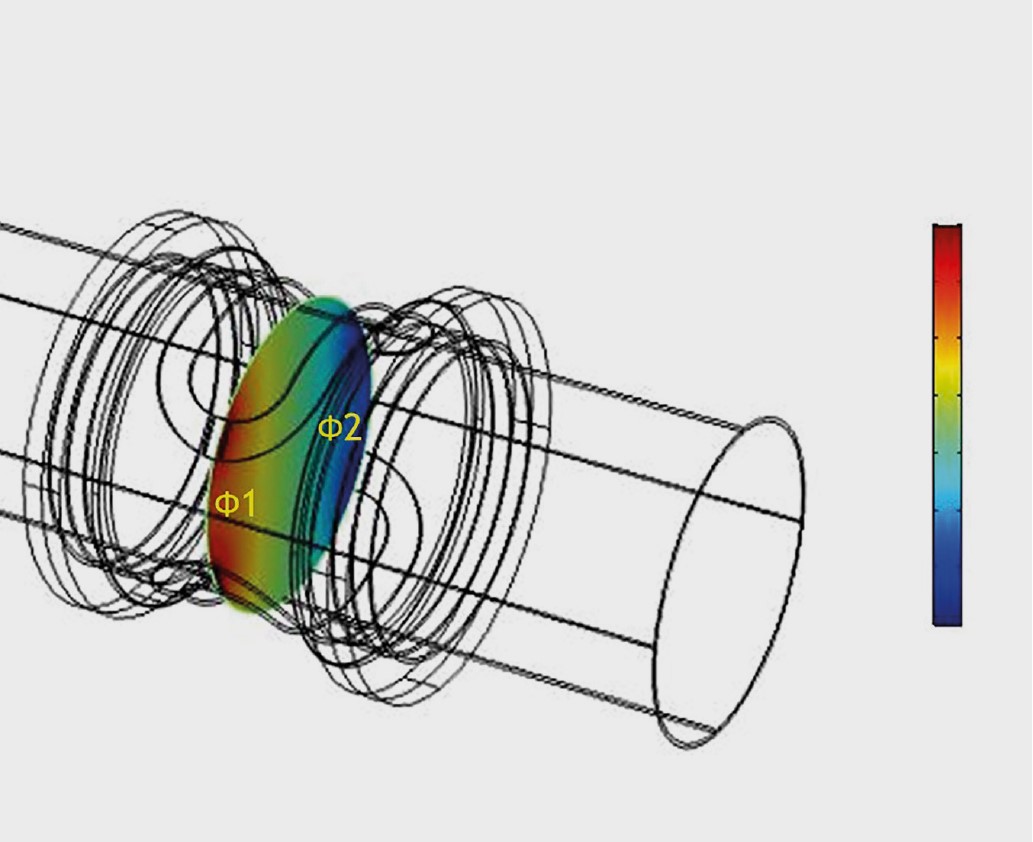
Figura 4. Valutazione dei fenomeni fisici in termini qualitativi; il rosso rappresenta i valori massimi. (A) Distribuzione del flusso magnetico. (B) Contorni di velocità del fluido. (C) Potenziale elettrico.
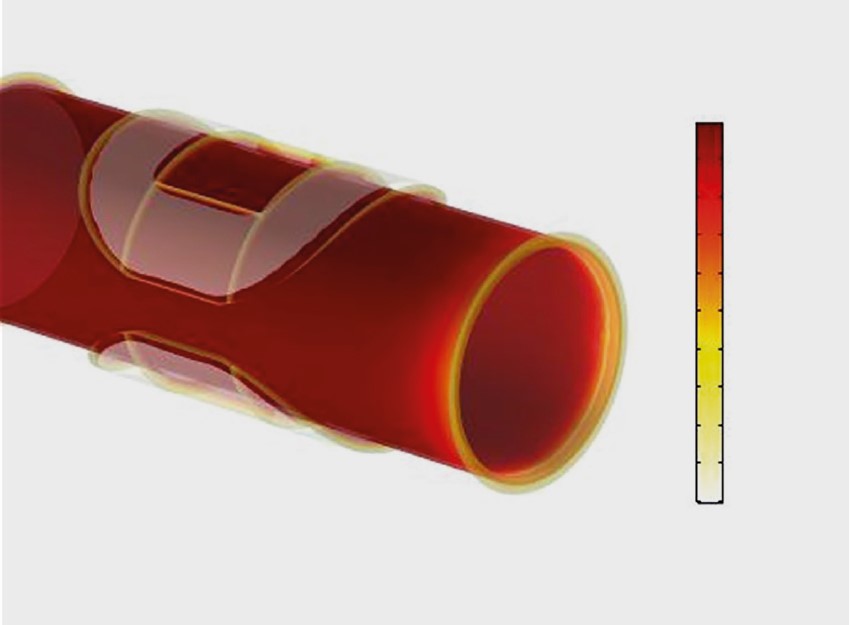

FIGURA 5. Illustrazione dei campi di sollecitazione idraulica e termica in termini qualitativi; il rosso rappresenta un valore massimo. (A) Campo di temperatura. (B) Campo di sollecitazione.
È evidente che la modellazione ha il vantaggio di ridurre al minimo la necessità di test, che sono costosi e richiedono molto tempo. Non solo il digital twin costituisce una risorsa durante la fase di test, ma il modello è stato anche ampiamente sfruttato per modificare il progetto esistente del flussimetro in modo da migliorarne la qualità. Incorporando nel modello progetti di nuovi componenti e idee innovative, è stato possibile valutare il miglioramento delle prestazioni del flussimetro.
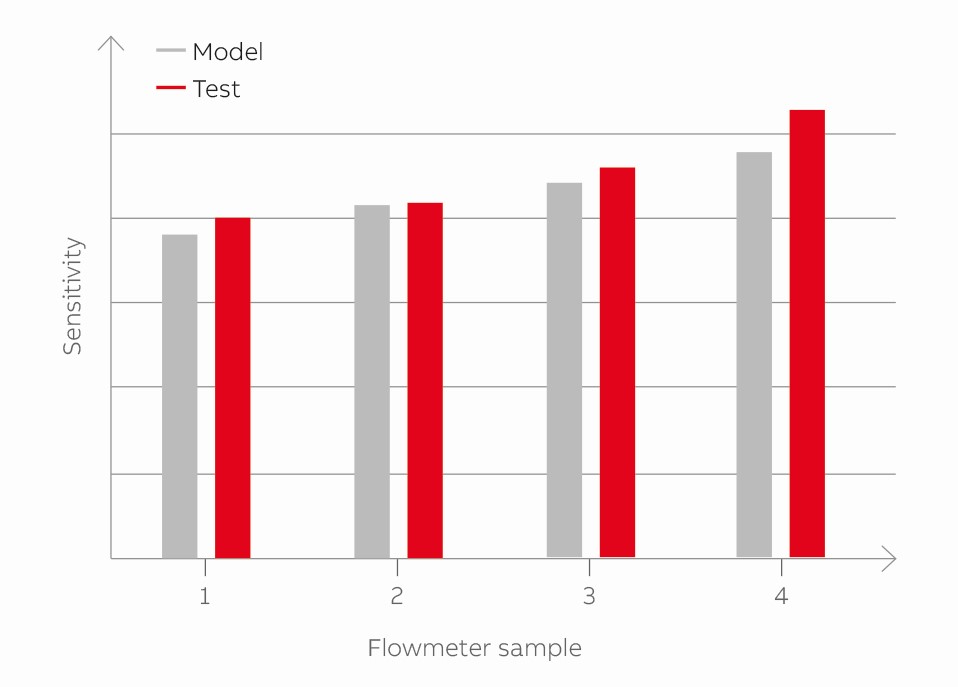
FIGURA 6. Diverse tipologie di flussimetri sono state modellate e confrontate con i dati ricavati dai test.
di Subhashish Dasgupta e Vinay Kariwala
Versione ridotta dell’articolo pubblicato originariamente su ABB Review (02/2018).


